Anyone who has ever experimented with Conway‘s Game of Life or any other cellular automata (CA) know they can be very fun to play with. You can easily lose several hours in e.g. George Maydwell’s awesome Modern CA site; his CA evolution lab is particularly cool. If you like to write your own CA code, there are some good efficiency hints on Tim Tyler’s CA page. (As a side note, Tim also has a good — but NSFW, due to boobie pic — rant on why the entertainment industry should be destroyed.)
While CA are fun, I’ve never been thoroughly convinced about their practical value; it always seemed like you could do the same thing with less effort. However, with all this GPGPU hysteria that’s brewing, perhaps it’s worth looking at them again soon. CA certainly fit fairly nicely onto a GPU.
In that I talked about pathfinding in my previous post, I thought that showing how CA could apply to pathfinding might be an interesting topic here, thus this post.
Solving a traditional maze
As my very first example, let’s look at how a CA can solve a traditional maze. By “traditional” I mean a maze with one entry and one exit, with a single path from entry to exit, and a path that’s one cell wide. Like this:

By considering the 4-neighborhood of a cell (i.e. the NSEW neighbors) we can use a CA rule that fills in a cell if we have 3 or 4 wall neighbors. What this will do is to effectively fill in the dead-ends of the maze from the “bottom”, one cell at a time, until every dead-end path has been filled. The figures below show the first iteration of this approach as well as the end result, after 24 iterations:


As should be clear, this CA fully solves the maze; the cells that remain unfilled constitute the path from start to goal. This method of solving a maze is well-known and is sufficiently obvious that it has been reinvented lots of times. (I rediscovered it myself sometime in the mid-to-late 80s I think, and I know others did too.) But we can do more interesting things with a CA than solving a traditional maze. As a small step forward, let’s look at a “fat” maze next.
Solving a “fat” maze
Here I’ve started with the same maze as before, but removed a lot of the walls and made some overall minor changes too. This leads to a maze where the paths are wider than one cell across, or — simply put — where the paths are fat:

To fill in dead-end paths in the fat maze we need a slightly different rule. The particular rule I’ll use here gives birth to a wall cell if, out of the 8-cell neighborhood we have:
- three wall edge neighbors (i.e. NSW, NSW, NEW, or SEW), or
- an edge neighbor (e.g. W) that 8-connects to a corner cell on the opposite edge (e.g. NE or SE) via a neighboring edge cell (here, N or S, respectively) — unless an opposite-edge corner cell exists but there is no neighboring edge cell to connect to it, in which case no new wall cell is birthed.
(Sorry, I know that’s a mouthful, but I can’t be bothered to draw a picture to illustrate. If that wasn’t clear, plot it out on graph paper, or hire me at my usual consulting rate of $350/hr for an elaboration!)
Running this rule on the fat maze gives the following results for iterations 1, 5, and 12 (where iteration 12 is the solved state):
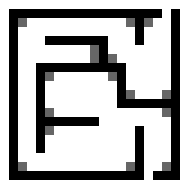
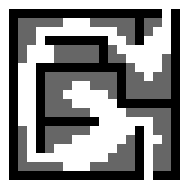

What’s cool is that it looks like we got the shortest path solution here. I haven’t played around with this rule enough (nor thought things through sufficiently) to know under what conditions we’ll get a shortest path, or indeed if the rule will always return a solution (as opposed to a set of cells containing the solution). If anyone has any insights, please add a comment!
Arbitrary pathfinding
We can also apply the same rule as on the fat maze to an arbitrary pathfinding problem, where we have a nonmaze and two arbitrary start and goal positions (here shown in red and green):

Running the rule on this problem gives on iterations 1, 5, and 12 the following result (with 12 again being the last state, the stable state detected on iteration 13):



Here, as expected, we don’t get an actual path on reaching the stable state. What we have achieved though is a pruning of the search space for a subsequent A* search (or similar), pruning away cells that we know do not need to be searched to find a path from start to goal.
Of course, this CA preconditioning step is today more expensive than running a full search over the whole space, but with things like GPGPU it might one day make sense to precondition the search space in this way for a subsequent pathfinding step. We can also amortize the CA cost by inserting multiple starts and goals (for multiple agents) before evaluating the CA to a steady state, so in some circumstances it might be worthwhile doing something like this already today.
BTW, there are other rules than the one I gave above, which prune even more of the search space, but will take away free cells that would be needed for a shortest path. But, then again, we don’t always care about a shortest path, do we now.
This approach reminds me of the fast marching method for level sets. There is a really cool Java demo by Sethian which shows how to do doing similar types of constrained motion planning operations, and practically speaking they are implemented in much the same way as a cellular automata. Here is the link:
http://math.berkeley.edu/~sethian/2006/Applications/Robotics/robotics.html
Searching for “level sets +GPGPU” predictably turned up a bunch of results on fluid simulation, but I couldn’t find any papers describing a fast marching method for the GPU (though I must admit that I didn’t look very hard). Could be interesting to see what happens if someone tries to take this idea beyond the java applet proof-of-concept.
Yo Christer, pretty cool! This seems similar to the thinning algorithms used in image processing. Knuth references Guo, Hall “Parallel thinning with two-subiteration algorithms”. in his write up on cellular automata. Also check out http://igm.univ-mlv.fr/LabInfo/rapportsInternes/2006/01.pdf
I had a go at implementing the maze solvers on the GPU. The traditional maze solver seems to work (it was easy enough!), but I can’t seem to get the fat maze solver to work. I probably made a mistake implementing it, but stepping through the generations it looks like the rules as I interpreted them are applied correctly. I’m beginning to wonder if this approach might not work with the parallel evaluation on the GPU, since it seems to be closing off the correct path from two sides in one generation (generation 3).
Anyway you can find the XNA/GPU implementation through the link above. I’d be much obliged if you could take a look at the shader (lines 164-260) to see if I managed to implement the rules correctly. Unfortunately your consulting rate is just a bit out of my league, but I’ll offer my everlasting gratitude :)
http://www.xnainfo.com/content.php?content=21
Hi Rim, cool to see you’re ambitious (read crazy) enough to attempt an implementation from that dense description of mine! I’m not set up to run C# on my PC, so I can’t run your code. (Basically, all Danish-designed programming languages are from hell, and I already have one too many Danish languages (C++) possessing my machine, so I’m not about to install C# even for this noble endeavor, sorry.)
Briefly glancing over your shader code though, it looks like you messed up the first rule (the “edgeNeighbors” calculation), for one. The first rule is to be read that if you have walls at three of the four 4-connected neighbors (N, S, E, or W), then fill the cell. That’s my fault for not describing the rule very well above. I’m afraid I didn’t try to decode your brave attempt at the second rule. I might give it a second glance later, but no promises.
BTW, I dunno if you can provide an .exe for the PC (that would be cool), but if not, it would at least be cool to see some screenshots from your code in action!
Hi Christer,
Call me crazy, but after seeing those fancy pictures I just had to have a go at it. Thanks for the prompt reponse, it looks like it was indeed the first rule I messed up. I reimplemented it and everything seems to be working out now. You can find a little movie (WMV) showing the maze solves over here:
http://www.xnainfo.com/file.php?file=87
As for an .exe, we typically try to avoid posting binaries, but I’ve uploaded a build to the link below. XNA does have a some prerequisite installs, which you can find listed at the 2nd link. The .cells files for the traditional and fat maze scenarios can be downloaded from the page I linked to in my previous post.
http://xnainfo.com/temp/GameOfLifeBin.zip
http://blogs.msdn.com/astebner/archive/2008/02/29/7968464.aspx
Fat maze automata is an interesting idea that could be used in a conditioning step so doesn’t need to be real time. Points of interest would become black cells so remain “accessable”.
Considering A-Star, what if an agents starts off in the gray area (such as random spawn point), of wishes to go to somewhere in the gray area (such as hiding). Or if an agent must travel through a gray area to reach its destination (I’m not sure if this last problem is even possible).
As a suggestion you could improve your description of rule 2, I can’t understand it at all. After looking at Rim’s shader I have written an implementation in C that solves the non-maze in 6 iterations (7th is stable). However the result differs from the one posted:
– Along the right hand edge. This seems to be due to the way it was solved, since the path left behind appears to have the same properties.
– Near the green square. This one I don’t understand.
http://img23.imageshack.us/img23/3997/automatang8.png
Hello, regarding this rule on turning a blank cell to a wall cell:
“an edge neighbor (e.g. W) that 8-connects to a corner cell on the opposite edge (e.g. NE or SE) via a neighboring edge cell (here, N or S, respectively) — unless an opposite-edge corner cell exists but there is no neighboring edge cell to connect to it, in which case no new wall cell is birthed.”
Can anyone help me understand why this rule exists/works? I understand the first rule regarding having 3 wall edge neighbours, but am confused by how anyone could even think of this second rule, let along understand why it works. I’m very unfamiliar with cellular automata, but have a basic understanding of pathfinding and some basic algorithms related to it, but yet I can’t seem to find much material on the Internet regarding using cellular automata to simplify mazes/pathfinding. Much appreciated if anyone could direct me to some material on this as well. :)