There are many possible collision geometry representations. One representation is the triangle soup: an unordered collection of triangles. The triangle soup is great in the sense it is easy for artists and designers to create, edit, and apply collsion materials to the triangles. A not-so-great property is that the triangle soup does not define a volume, so there is no way to dinstinguish between being inside or outside of the objects it represents — we can only detect collisions with the boundary. It therefore becomes very important to detect tunneling to avoid objects falling through the world. To detect tunneling we can, for instance, opt to use continuous collision tests. However, in games, many times we can get away with simply performing a line segment query from the start to the end position of the object’s movement.
Line segment and ray queries on the triangle soup are often also used for various noncollision purposes, such as testing for line-of-sight. So there are several reasons why we would want to support fast ray queries on the triangle soup. To accelerate line segment and ray queries (as well as other query types) against the triangle soup, we typically insert the triangles into some sort of hierarchical or spatial data structure. The k-d tree is a common choice (but others, such as grids or octrees, are also used). Queries are performed by traversing down the tree to the leaves whose spatial bounds are intersected by the ray. At the leaf, the ray is intersected against all the triangles stored in the leaf (which is usually on the order of 10-20 triangles, to get a good balance between tree height, memory requirement, query time, etc).
Storing 10-20 individual triangles in each leaf (or however many triangles there may be) really isn’t very good though. It throws away a lot of useful connectivity information that was likely present in the original dataset. Instead of storing triangles, a much better option is to store pairs of adjacent triangles. Like below, where we have two triangles, ABC and ADB, sharing the edge AB:
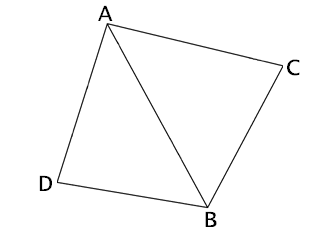
There are two nifty things about storing pairs of adjacent triangles instead of single triangles in the data structures I mentioned above:
- Memory is reduced by only storing (indices to) the shared vertices once (as opposed to twice).
- A ray or line segment can be intersected against the two triangles at virtually the same cost as intersecting against just one triangle.
The ray test is performed by doing sidedness tests of the ray against the edges of the triangles. By starting with the shared diagonal, we can skip testing the other two edges of the triangle we cannot be in, so only three sidedness tests are needed. The sidedness tests are done using scalar triple products (as I described in the Plücker post a while ago). For those needing more information, I talk about line vs. quad being the same cost as line vs. triangle in quite some detail in Section 5.3.5 of RTCD.
All we need to support both triangles and triangle pairs is an extra bit to distinguish between the two, and said bit can be easily found as e.g. the sign bit of a vertex index or similar. Easy peasy.
The astute reader will note that a pair of triangles with a shared edge is really just a special case of a fan or a triangle strip, so what I talk about here can be taken further by storing longer strips or fans, or using some other representation that maintains some connectivity information. Though strips or fans do not offer the simplicity of the triangle pair, where we save both speed and memory at the cost of just a few lines of extra code in tools and in runtime!
Next time you make triangle soup, try making it chunky – you’ll like the flavor!
hallo, a littel bit late…
i just read thru chapter 5 and found the idea of grouping triangles into more
complex stripes “expanding” and very useful to speed up of ray/triangle intersections.
is there also an optimized quad/line intersection available for double-sided quads ? a
simple halfspace test at the front will not work here to seperate the tris.