Range reduction (for trig functions)

There are lots of ways in which sine and cosine functions can be implemented on a computer. Often we see them implemented as polynomials (such as minimax polynomials) that are some infinite series truncated to the first few terms (perhaps between 3 to 10 terms depending on the desired accuracy). For example, on page 76 of Abramowitz’ and Stegun’s Handbook of Mathematical Functions we can find the following expression:

where

with constants

This error holds for 0 <= x <= pi/2. Note, this is not necessarily a particularly good expression for sin(x). For one, the polynomial coefficients are usually tweaked somewhat from the theoretical values to get a smaller error for a floating-point implementation. However, the above expression predates IEEE arithmetic, and will not have been tweaked for modern floating point hardware.

But the actual series and its error wasn’t what I was going to talk about. Intead I wanted to focus on the fact that these series always work on some limited range near zero. Of course, in a real application your inputs are rarely in the range expected by the approximation! For this reason the input value must be subjected to range reduction from the original range into this limited range. But while you can find lots of approximating functions all over the web, no one ever talks about range reduction and how it is performed! So, I thought I’d address that here.

There are two parts to performing range reduction for sine and cosine. The first part is to compute the reminder of the input argument modulo 2Pi, which we can do as both functions are periodic over 2Pi. If we don’t care too much about accuracy far from the origin, this can be done along the lines of this code:

float twoPi = 2.0f * PI;
float invTwoPi = 1.0f / twoPi;
int k = (int)(x * invTwoPi);
xNew = x - (float)k * twoPi;

(If we do care about getting accurate values far from the origin, you have to be a bit more careful in how this first range reduction is done, but I won’t go into this here, as this is not something that I personally care about in my applications.)

After running this code, x will now lie in the range -2Pi…2Pi. For e.g. sin(x) we would now have to deal with this part of the input domain:

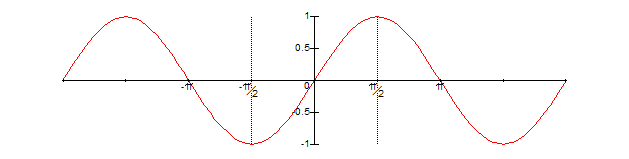
However, perhaps the polynomial we are using is only accurate within -Pi/2..Pi/2 (the region between the two dashed lines). What to do? The trick is to realize that we can fold the input argument back “over itself” around symmetries in our target function. Note that sin(x) is symmetric about e.g. Pi/2, so what we can do is subtract Pi/2 from x, giving:

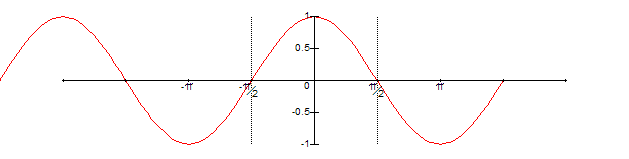
We then let x = -Abs(x), folding the input arguments “to the left” about 0, resulting in:

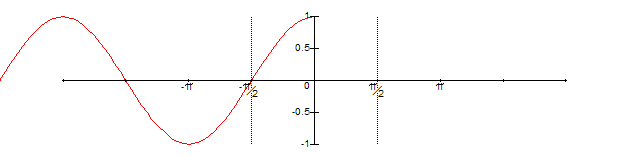
We finish off by adding Pi/2 back in to get:

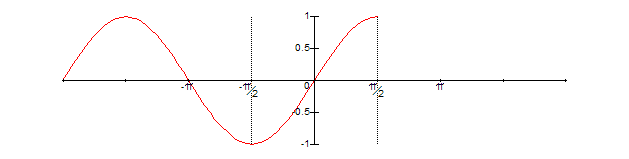
Combined, these three steps are x = -Abs(x – Pi/2) + Pi/2. As Abs(x) = Max(x, -x) and -Max(x, -x) = Min(-x, x), the folding operation we just did can also be written as x = Min(x, Pi – x).

Analogously, we can now fold the input argument to the right across -Pi/2 by performing the operation x = Max(x, -Pi – x), giving:

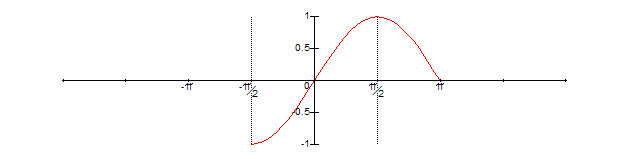
This last operation results in a small part of the input argument extending past Pi/2, so we need to perform the folding x = Min(x, Pi – x) one more time, to get the final, desired, result:

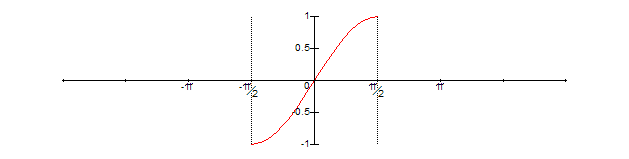
At this point we have sucessfully range reduced the input argument from -2Pi..2Pi into -Pi/2..Pi/2 (the range for which our hypothetical sine approximation function had the best accuracy) by doing the following three operations:

float x = ...;
x = Min(x, PI - x);
x = Max(x, -PI - x);
x = Min(x, PI - x);

Finally, there are two neat things worth noting about using Min and Max (or Abs) to do the folding. These are often available as native SIMD instructions, so not only do we not need to do any branches, but we can perform four range reductions (and subsequent sine or cosine function evaluations) in parallel!