Artists get a lot of mileage out of animating the alpha reference value for the alpha test. Lets call the alpha reference value t. Then, for example, by having alpha come from a 0..1 alpha “contour” or “depth” map, artists can make things gradually appear or disappear by animating t.
What the alpha tests implements is effectively the Heaviside step function, except centered at t instead of at 0. You also find this implemented e.g. in the step() function of the Renderman shading language:
float step(float t, float x) {
return (float)(x >= t);
}
The alpha test is great for cutout alpha, but if you have a shader system that does layering within a single shader, having a “reference alpha” feature for the blending of each layer in the shader also makes a lot of sense. We can easily implement the step function in a shader as per above, but it is easy enough to support a small palette of alpha filtering functions that an artist can apply to the alpha values read from an alpha channel (or similar).
The picture below shows a few interesting functions to map an input alpha, x, into an output alpha, y, with control parameters t and w:
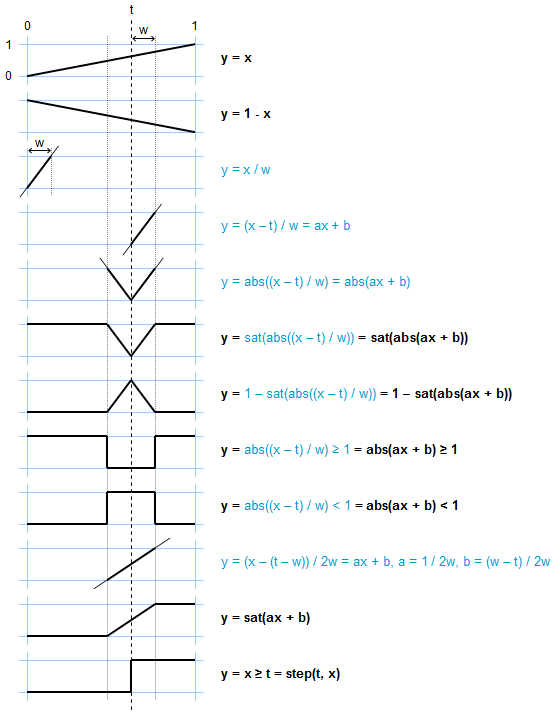
The last function above is the traditional step function. (The functions in blue can be ignored; they are only there to help show the function derivations.)
It is worth noting that the square pulse() function can also be implemented in terms of subtracting two step() functions:
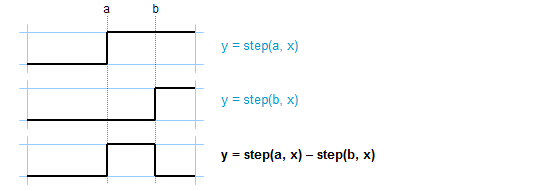
We can use the same technique to come up with expressions for most of these functions. For example, the triangle pulse can be expressed as:
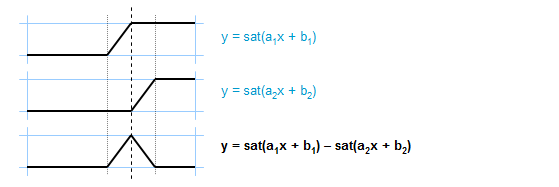
In addition to these simple functions that can be implemented in around 1-3 shader “instructions”, we can also provide smooth filtering functions. I’m not covering the smooth functions here, because, well, I don’t have a nice way of plotting them accurately!
That said, at least be familiar with the smoothstep() function:
float smoothstep (float min, float max, float x) {
x = saturate((x - min) / (max – min));
return x * x * (3 - 2 * x);
}
(Follow the link to see what it looks like.)
Which functions does your engine support?